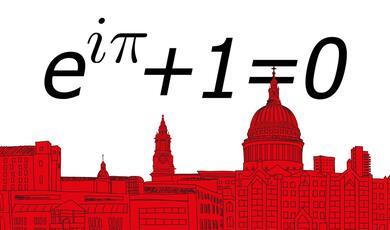What have Mathematicians Done for Us?
Share
- Details
- Text
- Audio
- Downloads
- Extra Reading
Mathematics has played a vital role in the development of human civilisation, and is the foundation of much of modern technology and popular culture. However, the achievements of mathematics and mathematicians are often unknown or misunderstood. The contribution of mathematicians over the centuries will be celebrated, showing how mathematical ideas have huge relevance today – varying between Maxwell and the mobile phone, Florence Nightingale and modern statistics, Pythagoras and the development of music, Euclid and art, Euler and Facebook, and Cayley and Google. Even basic mathematics can make a profound difference to our lives.
Download Text
11 October 2016
What have Mathematicians Done for Us?
Professor Chris Budd OBE
Introduction
On the whole, mathematics and mathematicians has a rather bad image with the general public, the media, and (sadly) policy makers. It is often thought of as being remote, inaccessible, and of no possible use to anyone. Similarly, mathematicians are regarded as cold, unemotional, mad, male nerds. People seem so frightened of mathematics that in a recent event, an aircraft was delayed because someone on it saw a Professor working on a differential equation and alerted the cabin thinking that he must be a terrorist http://www.bbc.co.uk/news/world-us-canada-36240523.
This caricature of mathematics, and of mathematicians, is not only false: it is grotesquely untrue. In contrast to its perceived uselessness, mathematics has played an essential role in the development of civilization, and lies at the heart of all modern technology. Things we now take for granted: the mobile phone, the internet, credit cards, satellite navigation, radio and TV, weather forecasting, radar, train scheduling, and even microwave cooking. All these could not function at all without the application of clever and careful mathematical algorithms. It is these aspects of mathematics that I want to explore not just in this lecture, but in all of the lectures in this series.
Part of the problem is that few people really know what mathematics is, or what it can do, beyond the use of simple arithmetic which terrified them at schools, and is now largely done by calculators (which has led some people to claim that mathematics as a subject no longer exists). This confusion even extends to mathematicians themselves who tend to flounder around when trying to define their own subject. (A glance at the Wikipedia page on mathematics does not help when trying to define it). One definition that I like is that mathematics is all about patterns which link different objects together. Another is that maths is what mathematicians do. (Which I personally find very unsatisfactory). But my favourite definition (by far) is that maths is the subject in which we can write down, and make sense of, statements like this:
π/4=1-1/3+1/5-1/7+1/9-1/11+⋯
Isn’t that wonderful! This beautiful and unexpected formula links , the ratio of the circumference of a circle to its diameter, to the odd numbers. It was derived by the Indian mathematician Madhava of Sangamagrama in the 14th Century, and later rediscovered in the West by Leibniz and Gregory at the dawn of the invention of calculus. Arguably, the truth inherent in this formula is eternal. Anyone not stunned by it has (in my opinion) no soul. As we shall see, formulae such as this play a vital role in modern technology, as does the number itself. However, it is not obvious how to go from such seemingly abstract works of beauty to the technology of the modern world, nor how to use maths to unravel the secrets of the universe. This is the topic I want to explore in this lecture, through a series of carefully chosen examples which I will develop in the rest of this lecture series.
However, it is not maths which has made the modern world: it is mathematicians. School maths text books usually display it as a dry, logical subject, with no human content. They frequently ignore the people that created maths in the first place and the stories behind them. This led to one school child I was talking to saying “I don’t do maths, because I’m a people person!” It might possibly surprise them to know that I’m a people person myself and that (with possibly one or two exceptions) mathematicians are people too. In fact mathematics is full of examples of exceptional people whose achievements really have changed the world that we live in. Sadly most of these, except possibly Archimedes, Isaac Newton, and Albert Einstein, are unknown to the public or if they are known are not recognized as being mathematicians. Leonhard Euler, Carl Friedrich Gauss, William Kelvin and Évariste Galois, are all giants of mathematics, but who in the general public knows about them?
One of the exercises I often do when talking to school children is to put up a picture of a mathematician who I can guarantee has changed all of their lives, and for them to tell me who it is. The picture I put up is that of James Clerk Maxwell. It was Maxwell, by mathematically unifying the three subjects of electricity, magnetism and optics, discovered (purely by mathematical reasoning) the existence of radio waves and thus ushered in the modern world. Without radio waves we wouldn't have mobile phones, WiFi, the Internet, computers, radar, Google, Sat Nav or any of the paraphernalia of the modern world. As I said, Maxwell has utterly changed the world we live in today, but no one seems to know who he is. (Maxwell was in many ways a very interesting person, and did many other things besides, including inventing colour photography, and deducing the structure of the rings of Saturn). Another exercise is to ask the same group to name a female mathematician who has changed the world and who they all know. Usually I am treated with the name of a TV celebrity. Very rarely does someone come up with the name of Florence Nightingale! But it was Nightingale who basically invented the subjects of medical statistics and the graphical representation of data. Indeed it can be argued that she was the forerunner of the Big Data Revolution that I will talk about in my next lecture.
I think that the real problem that (applied) mathematics, and the (applied) mathematician, faces is that like the air we breathe, it is vital for all that we do, but it is invisible and easy to ignore. Hopefully this talk will make the role of mathematics a little more visible. Ultimately I want to address the issues raised in quote from Edward David, former head of Exxon Research and Development, who said, in a report to the US Government:
“Too few people recognize that the high technology so celebrated today is essentially a mathematical technology”
I will do this by showing how mathematical technology really works.
The mathematical process, or how does applied mathematics work?
My job title is Professor of Applied Mathematics. But what does this mean? One view of mathematics (sadly believed by many of my colleagues) is that there is a factory called Pure Mathematics, which creates maths, as an abstract concept unconnected to the real world. The job of the applied mathematician is to then take this and to find real world situations where it might be useful. I personally believe this to be at best an oversimplification, and at worst wrong. Applying mathematics to the real world is hard, and nearly always you have to invent new maths to solve practical problems. This mathematics, and the related mathematical tools, can then be abstracted leading to the discovery of new questions, patterns, structure and ultimately theorems. The wonderful thing is that these theorems can then be used to help solve many other problems, which can look very different. Great mathematicians such are Carl Friedrich Gauss, Emmy Noether, Leonhard Euler, Bernhard Riemann, David Hilbert and John von Neumann certainly all had this view of mathematics, seeing no distinction at all between what is ‘pure’ and ‘applied’. Thus (applied) mathematics can be seen as a way of finding a bridge, which transfers ideas from one very different area to another, and creating new ideas along the way. A classical example of this is calculus, which had its roots in the need to solve problems in celestial mechanics, and now in its refined and abstract form gives us insights into nearly every problem in the physical, biological and even social sciences. Another supreme example is Euler’s fabulous theorem:
e^(i π)+1=0
Not only is this (as voted by the majority of the world’s mathematicians) the most beautiful formula in mathematics, it is also the central formula for any problem involving waves or rotational motion. Whole books have been written just about this one formula [4].
Now let’s see how this all works by looking at a brief history of some of the ways in which maths has made the modern world. To do this I have chosen a series of mathematical achievements, which have all impacted the world in a number of ways, starting from the ancients and moving up through the centuries. I hope that by doing this we will see both how maths made the modern world and how the making of the modern world has stimulated much of modern mathematics.
Early maths, Quadratic equations and the tax man
We believe that early humans counted on their fingers. This led directly to the concept of the natural numbers 1,2,3,4,... From these we have built the rest of mathematics, as we now know it. Note that I have used the word built. Maths is above all a highly creative subject!. The natural numbers when extended by the negative numbers and 0, give us the integers. When ratios are taken of these such as 2/3, -3/4, or 7/11 we get the rationals, and when you take limits of sequences of rationals you get real numbers such as etc. Problems which are solved in terms of integers (or perhaps rationals) are often called discrete, and those which involve real numbers are often called continuous.
The original problems in mathematics were all discrete such as ‘I have 6 cows and I sell 4, how many do I now have’. One of the first professions to look into the solution of such problems was, inevitably the tax man. Whether or not this is the first example, it is certainly one of the first recorded examples, as we might expect from the tax profession. The earliest medium in which such mathematics was recorded was cuneiform writing on clay tablets, and it was written down by Babylonian scribes. Many examples of such tablets can be found in the British Museum, and they give a fascinating insight into the impact of mathematics on the ancient world, and in particular the growth of the early city state (and the large armies associated with it!). Discrete problems continue to be very important in modern technology, and lie at the heart of modern digital technology, which uses natural numbers to represent music, pictures, and even films and exploits properties of the integers to represent, store, manipulate and transmit these in an error free manner.
However, the Babylonians rapidly found that not all of the problems of interest to them were discrete. A number of these tablets concentrate, instead, on the continuous problem of the) calculation of areas. This was again mainly for the benefit of the taxman, who would be assessing the size of fields to determine the level of tax for each, which was proportional to the area of the field. One question they posed was what by proportion should the size of a field increase by if its area was to then double. To find the answer to this problem requires solving the quadratic equation . Remarkably the Babylonians were able to fund a very good approximation to the solution (x = 1.41421356237…) of this equation. This and many other solutions of different quadratic equations (all of value to the tax man) could be found in extensive tables, which were the forerunners of the navigational tables we will describe shortly.
Later on, continuous problems became more important as a way of describing the real world. Continuous problems still have this importance, indeed the calculus developed by Newton and Leibnitz in the 17th Century is based on them. Nature abounds with lovely examples of patterns and order, all of which much have inspired in our earliest ancestors the feeling that there was some structure in the universe which could perhaps be explained. The ideas of calculus can be found in the order of the waves on the sea, the motion of the stars and planets, the regularity of the seasons, the shape of clouds, the geometry of crystals, the arc of a rainbow, the hexagons in a beehive, the (fractal) shape of a lightning bolt, and much more. Calculus continues to be the best tool we have to understand the modern world and to predict the future.
Maths for recreation, and why this can be serious
Maths isn’t always thought of as fun, and it certainly isn’t usually taught that way. However mathematics actually lies behind many areas of recreation and culture and it enriches our lives by doing so, even if you are not a mathematician, or even realize that you are doing maths.
Mathematical puzzles as a form of recreation have been around almost as long as maths itself, see [5] for lots of great examples of this. Indeed some of the deepest problems in maths were originally posed as puzzles. A good example of this being the problem of ‘doubling the cube’ (i.e. finding a cube which has twice the volume of an original one), which it is claimed was posed by the Oracle of Delphi. Another example of an early recreational puzzle is the maze. The earliest maze (technically a labyrinth) recorded in literature can be found in the celebrated story of Theseus and the Minotaur. In the 17th Century the puzzle maze became very popular as a recreational fashion item in gardens across the world. Now we see the mathematical process at work. The recreational stimulus of solving the maze (i.e. finding the way to the centre and back again) occupied the minds of some of the leading mathematicians of the age, and was essentially solved by Euler, who devised the theory of networks to do it. Network theory now has important applications in the study of communications (such as the Internet and Google), the spread of epidemics, the propagation of rumours, the spread of Social Media, and even the voting patterns in the Eurovision song contest. One way to represent a large network, such as the World-Wide-Web, is to draw up a (very large) square table with each side listing all of the web sites in the world (yes there are billions of them) with a 1 if one web-site points to the other, and a 0 otherwise. Such a table is an example of a matrix, which was a mathematical object developed and studied by Cayley in the 19th Century. Matrices have applications in just about every branch of maths, physics and engineering. For our current purposes, without Cayley’s invention we would not have Google. I return to this subject in more detail in the next lecture.
Another problem Euler was interested in was that of Latin Squares. These were square, made up of many smaller squares to form a grid, with numbers arranged in the grid such that each number appeared once in each row and column of the grid. If that sounds familiar, then it is. It is the basis of all Sudoku puzzles, which engage a huge number of people, all of whom are using some form of mathematical reasoning to solve them. Whilst purely recreational, the methods used to solve a Sudoku puzzle are closely related to techniques for scheduling (for example) aircraft, buses and trains, and constructing a school timetable. Finding efficient algorithms to do this is both very important and very hard. Indeed the question of finding the best algorithm (and showing that it is the best) is one of the hardest unsolved problems in modern mathematics.
Maths appears in many other games, ranging from Mornington Crescent [1] to game shows such as Deal or No Deal. Many of these games require an estimation of risk and a strategy for responding to your opponents moves. The study of related situations involving two players led John von Neumann, and later John Nash, to develop the mathematical Game Theory which is now used to inform decision making by economists, business leaders and even governments, all of which greatly impact on the modern world. Indeed it played a central role in the recent telecoms auctions where multiple millions of pounds changed hands.
As a finale to this section on recreational mathematics, I can’t resist making a brief mention of the role that mathematics plays in music. Everyone has heard of the Greek mathematician Pythagoras who is credited (falsely) with the discovery of the famous theorem named after him about the sides of a right angled triangle. Less well known is that Pythagoras made a study of music, and made the momentous discovery that the frequencies of two notes which sounded pleasant when played together were in a rational proportion. For example the ratio of the frequencies of the notes of the Octave (C:C) is exactly 2 and of the Perfect Fifth (C:G) is 3/2. From this observation he went on to construct a sequence of notes all of which sounded good when played together, and which had notes in rational proportion. This sequence e.g. C:D:E:F:G:A:B:C we now know as the scale. In particular, the Just Scale is the sequence in the ratios:
1 : 9/8 : 5/4 : 4/3 : 3/2 : 5/3 : 15/8 : 2
This creation of the mathematical mind served musicians well until the 18th Century. Around this time the first keyboard instruments came into use. These were tuned once and for all, and the tuning could not be changed by the player. It was rapidly found that a keyboard instrument tuned to the Just Scale in one key would sound out of tune in other keys. The solution to this problem was to introduce a new scale in which the notes were all in equal proportion. In particular, as there are 12 semi-tones in the octave, the ratio of the frequencies of successive semitones was 1.0595… which is the twelfth root of 2. Keyboard instruments tuned in this (mathematically based) equally tempered scale sounded in tune for every key, and the new scale was rapidly adopted. Bach was so pleased with it that he wrote The Well-Tempered Clavier to celebrate a really nice application of mathematics to the art of music.
Maths tells you where you are.
Perhaps the leading scientific question of the 17th and 18th centuries was the question of finding Longitude at sea. It had almost a mythical status and appeared in Gulliver’s Travels as an example of an impossible problem. This difficult question not only stimulated a lot of mathematics, but also led, directly, to the modern world in which mathematics and machines work together.
The first breakthrough in navigation came when it was realized that the position of the sun and the stars in the sky depended upon where you were on the (round) Earth. By seeing how the angle of the sun changed the Greek mathematician Erastothsthenes was able to calculate the radius of the Earth to surprising precision. Having worked out a coordinate system for the Earth (Latitude and Longitude) it was apparent that the latitude could be determined by measuring the angle of the noonday sun above the horizon. Doing this in itself required a good knowledge of angles and trigonometry. The angle itself could be measured using a sextant, again using ideas from trigonometry. At that point the mathematics became much harder. In order to find the longitude it was necessary to determine the time at the location with reference to some absolute standard. Mathematicians such as Newton struggled with this problem, and in a sense solved it, in that they found that the longitude could be determined from very accurate measurements of the location of the moon, combined with a fearsome amount of calculation. Unfortunately, none of this was possible in the conditions at sea (and before the invention of the pocket calculator). An accurate method of finding longitude had to wait until the development of the chronometer H4 by Harrison as a means of finding the time at Greenwich. See Sobel’s book [7] for an excellent account of Harrison’s struggles to build this first chronometer. However, even then a large amount of calculation was needed and here mathematics came into its own. In particular the development of spherical trigonometry, which was needed to solve the triangles on the surface of the Earth that were the results of the navigational measurements. (Further careful mathematics was needed to make the necessary corrections for refraction, parallax and dip.) Tables were constructed which solved triangles with a vast range of different angles. These were used in parallel with Ephemerides, which were tables of the location of the Sun, planets and many stars for frequent time intervals in every day throughout the year. Looking at nautical tables from the 18th Century I am overwhelmingly impressed by the amount of calculation needed to produce them, most of which would have been done by human ‘computers’.
The result of all of this mathematics, combined with the mechanical brilliance of Harrison, was completely transformative. It utterly transformed navigation by sea, making it much safer and cheaper to transport goods around the world. By doing do it revolutionized both the economy and also the process of exploration, leading to the modern world.
There was a nice side product of all of this effort. The process of producing the navigational tables was essentially routine and open for being mechanized. Driven by this idea, in the 19th Century, Charles Babbage was inspired to design the difference engine arguably the ancestor of all modern computers. Sadly, Babbage did not live to see his machines actually working (although a working model of the difference engine was built by the Science Museum), but his ideas have certainly led to the modern computer, and thus the modern world.
Fourier, his series, and where it led to
One of the nicest examples of a branch of maths devised to solve one problem, which then solves many other problems is that of Fourier series. Joseph Fourier was a 19th Century French mathematician who was interested in how heat flowed through a body. His first contribution was in devising, what is now known as the heat equation to describe this. Fourier’s equation was an example of what is called a partial differential equation and it described the way that the temperature T of a body depended both on time t and space x. In modern notation, Fourier’s equation (now usually called the heat equation) is:
∂T/∂t=k (∂^2 T)/(∂x^2 )
Where k is the thermal conductivity. Fourier then set about solving this equation. His first extraordinary insight was that he could solve it by expressing T as a sum of simple functions and then finding the solution in terms of these functions. A good way to think of this is that it is much easier to build a house brick by brick, than to build it in one go. His second extraordinary insight was in his choice of functions to construct the temperature out of. His choice was to use the sine and cosine functions, which arise in trigonometry (the study of triangles) so that he wrote down the expression for T as:
T(x,t)=1/2 a_0 (t)+∑_(n=1)^∞▒〖a_n (t) cosnx+b_n (t) sinnx 〗
(This expression is now called a Fourier series). At first sight this is an extraordinary choice of a way to represent T. After all, what was the possible link between triangles and the flow of heat? However, it was exactly the right choice to solve the heat equation above. It allowed to problem to be broken down into a set of much simpler problems, each of which could then be solved and combined to find the solution of the original problem. In fact it was found shortly after this original insight that the use of sines and cosines to build up a function could solve a huge number of other problems as well, including: the motion of waves, the behaviour of gases, many problems in gravity, electrostatics, electromagnetism, and even the behaviour of the stock market. This exactly illustrates my earlier point that mathematical ideas used to solve one problem (the shape of triangles) could be used in others which seem at first sight to have no connection with the original. Following Fourier’s great discovery many mathematicians got to work on extending and generalizing his idea, finding many nice results on the way including a slick derivation of the wonderful formula (originally discovered by Euler):
π^2/6=1+1/2^2 +1/3^2 +1/4^2 +1/5^2 +1/6^2 +1/7^2 +⋯
Fourier series, and their discrete generalisations on a computer, play a fundamental role in modern technology. In particular we use them to make up, and process, sounds, information and images, and the music, TV and video industry would not exist without them. To learn more about the history and applications of Fourier series see Korner’s book [3]
Maths saves lives
My sister is a consultant doctor and I am very proud of her. Hopefully through her work she saves many lives. We think of doctors and nurses as occupations which save lives, and this is of course true. However, mathematicians save lives too. We have already talked about the great statistician Florence Nightingale, who saved thousands of lives by combining statistics with nursing. Her work continues today with the careful use of medical statistics to quantify the effectiveness (and potential risk) of different medical treatments through clinical trials, and ruling out the use of possibly dangerous treatments. Mathematics is also used in my sister’s field of anaesthetics, where it plays a vital role both in determining the correct dose of the anaesthetic and also (through statistics again) determining its effectiveness.
However my favourite application of mathematics to medicine (and also the one I am most closely involved with) is that of medical imaging. Until recently, if something was wrong with you, the only way to find out the problem was to cut you open. Such a procedure was fraught with difficulties. It was usually hard to find the problem, it damaged the body and left it vulnerable to infection, it could usually only be done once, and for parts of the body such as the brain it was quite impossible. The situation today has been completely transformed. Through medical imaging techniques ranging from Ultrasound, Computerised Axial Tomography (CAT), Magnetic Resonance Imaging (MRI), and Positron Emission Tomography (PET) doctors can see very precisely what is going on inside your body (including your brain) without ever having to cut you open. Indeed, with the recently developed Functional MRI (fMRI) methods it is even possible to monitor your brain in real time, and thus get an insight into what you are thinking. Millions of scans of people are made every year, and they save countless lives.
The initiator of this medical revolution was the Austrian mathematician Johannes Radon. If you look at a picture of Radon he looks just like you would think a mathematician should look like. He is old, white, balding, short-sighted and has a moustache. In pure mathematics he has a huge reputation for his work in the (difficult) field of measure theory. As part of his work in this, in the early part of the 20th Century, he asked the seemingly abstract question of what information could you learn about an object by looking only at the shadows that it cast from a distant light source. He published a paper in 1917 describing what is now called the Radon Transform linking an object to its shadows, and showed that although shadows are (only) two dimensional projections of a three dimensional body, that if enough measurements were made it was possible to reconstruct the original three dimensional object. So far, so abstract. However, at around the same time that Radon was doing his mathematical work, X-Rays were increasingly being used (recall that this was also during WWI) to diagnose medical conditions without having to cut open a body. However, the image given by an X-Ray was effectively a shadow of the body and lacked most of the detail needed for diagnosis. It took fully fifty years to combine Radon’s ideas with the technology of X-Rays, and this was finally achieved. The story of how this happened is remarkable in itself. Following Radon’s work other mathematicians developed faster ways of reconstructing the three dimensional object, most notably Kaczmarz in the 1930s. Using these ideas, the first commercially viable X-ray (CAT) scanner was invented in 1967 by Hounsfield at the EMI Central Research Laboratories using X-rays. The first EMI-Scanner was installed in England and produced the first brain-scan 1971. (It is rumoured that the funding for this came from the sales of the Beatles’ records). Almost independently, Cormack in the USA invented a similar device based closely on Radon’s ideas (which Cormack said he had discovered independently). Cormack and Hounsfield were jointly awarded the Nobel Prize in 1979. Sadly there is no Nobel Prize for mathematics. However, it is nice that you can still win a Nobel Prize for applying mathematics to the world.
Radon’s wonderful transform for a body of density f(x,y) is given by:
R(ρ,θ)=∫▒〖f(ρ cos(θ)-s sin(θ),ρ sin(θ)+s cos(θ) ) ds〗
Here R is the measured intensity of the X-ray at an angle to the body and a distance away from it at its closest point of approach. The integral expresses the way that the X-ray is absorbed, and the function f(x,y) tells us what is going on inside the body. Basically, if you know R well enough then you can find f(x,y) and then work out what is going on inside the body. Anyone who has solved a Griddler puzzle in a newspaper in order to find a hidden picture is basically doing this calculation themselves.
If I were to write Radon’s formula on an aircraft I might (possibly as we have already seen) get arrested for being a terrorist. But by doing so I might be helping to save many peoples’ lives.
We will return to the topic of medical imaging and how Maths Saves Lives, in much more detail in a later lecture, but you can read more in [?].
The world of communication
A defining aspect of human society throughout the ages is our need to communicate. This trend has accelerated a great deal in recent years, with our instant access to huge amounts of data and the ability to communicate over vast distances via mobile phones. Sometimes we want our communications to be secret (such as when we send credit card details over the Internet), and sometimes we want them to be as clear as possible (such as when we use a mobile phone to talk to someone in Australia). However, none of this would be possible without mathematics. The business of secret communications started with the early ciphers used, for example, by Julius Caesar. Although Caesar was not a mathematician, his ciphers certainly had a mathematical basis, in this case addition modulo 26. Since then mathematics has played a part in nearly all ciphers. A famous example was the machine based Enigma cipher developed by the Germans in the Second World War, and due to its complexity it was thought to be unbreakable. As is now well known, a team of mathematicians at Bletchley Park, including Alan Turing and Bill Tutte, managed to exploit mathematical patterns in the Enigma machine to crack the cipher. This changed the modern world in many ways. First the obvious, had they not cracked the ciphers the Allies may well have lost the war. Secondly, the method of cracking the ciphers involved computers, and the design of the code breaking Colossus electronic computer by Tommy Flowers ushered in the modern computer age. Modern ciphers, such as the RSA cipher, also rely very heavily upon mathematics, especially the ‘pure’ mathematics of prime numbers. For example it is easy to multiply two large prime numbers together, but very hard to find the original two primes given the answer. This asymmetry is used in modern public key ciphers, which are used millions of times every day to keep communications secure. See [6] for more details.
Personally I find the whole business of security rather dark and I much prefer the subject of making communications as transparent as possible. One of the most important side products of the space race (apart of course from non-stick frying pans) was the development of Error Correcting Codes. In order for a satellite to send back information through a noisy channel and across the vast distances of space, it was essential to find a robust way of making sure that the information got through without error. The answer was again provided by mathematicians, in particular Claude Shannon and Richard Hamming, working at Bell laboratories. Shannon’s seminal contribution was to develop the theory of communication, in which it was possible to predict how much information could be sent through a noisy channel. Hamming’s equally important contribution was to work out how to send this information so that if an error occurred the computer receiving it could correct the error itself. In a landmark paper in 1950, he created a family of error-correcting codes now called Hamming codes. These work by creating digital symbols for the different parts of a message which are so different that even if one is corrupted by noise it can still be told apart from any other symbol. The original symbol can then be restored by the computer, and the message corrected. This wonderful idea (which interestingly used mathematics created by the French mathematician Galois in the 19th Century) not only solved the particular problem of communicating a message over long distances, but also opened up a whole new branch of mathematics, that of coding theory. Error correcting codes are now used everywhere, without them we would not be able to transmit pictures or documents over the Internet, phone long distances on a mobile phone, or even listen to music on a CD. Truly they lie at the heart of the technology of the modern world.
I will return to many of these issues in more detail in my next lecture, which will be on the mathematics and relevance of Big Data.
And where next
This brief overview of what mathematicians have done for us is meant mainly to whet your appetite. Later on in this series we will see many more applications of mathematics to the modern world, and I will explore both how the latest developments in maths are likely to lead to even newer technologies, and also what new maths I expect we might learn, stimulated by these technologies.
Some References
[1] C. Budd and J. Budd, How to win at Mornington Crescent, (2016), Plus Maths Magasine,
https://plus.maths.org/content/how-win-mornington-crescent
[2] C. Budd and C. Mitchell, Saving lives: the mathematics of tomography, (2008), Plus Maths Magasine, https://plus.maths.org/content/saving-lives-mathematics-tomography
[3] T. Korner, Fourier Series, (1984), CUP
[4] P.J. Nahin, Dr Euler’s Fabulous Formula. (2011), Princeton
[5] W. Rouse Ball and H. Coxeter, Mathematical; recreations puzzles and essays, (2016), University of Toronto Press.
[6] S. Singh, The code book, (2010), Harper-Collins
[7] D. Sobel , Longitude, (2011), Harper-Collins
© Professor Christopher Budd OBE, 2016
This event was on Tue, 11 Oct 2016
Support Gresham
Gresham College has offered an outstanding education to the public free of charge for over 400 years. Today, Gresham College plays an important role in fostering a love of learning and a greater understanding of ourselves and the world around us. Your donation will help to widen our reach and to broaden our audience, allowing more people to benefit from a high-quality education from some of the brightest minds.


 Login
Login